https://accounts.google.com
Popisky snímků:
Kapitola 9. Základy matematické statistiky, kombinatoriky a teorie pravděpodobnosti §54. Náhodné jevy a jejich pravděpodobnosti 3. NEZÁVISLÉ OPAKOVÁNÍ TESTŮ. BERNULLIHO TEORÉM A STATISTICKÁ STABILITA.
Obsah PŘÍKLAD 5. Pravděpodobnost zasažení cíle jednou ranou ... Řešení 5a); Řešení 5b); Řešení 5c); Řešení 5d). Všimněte si, že ... V celé sérii opakování je důležité vědět ... Jacob Bernoulli spojil příklady a otázky ... VĚTA 3 (Bernoulliho věta). PŘÍKLAD 6. V každém z bodů a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost Pn (k). Řešení 6 a); Řešení 6 b); Řešení 6 c); Řešení 6 d). Bernoulliho věta umožňuje ... VĚTA 4. Pro velký počet samostatných opakování ... Pro učitele. Zdroje. 2.8.2014 2
3. NEZÁVISLÉ OPAKOVÁNÍ TESTŮ. BERNULLIHO TEORÉM A STATISTICKÁ STABILITA. Část 3. 2. 8. 2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 3
PŘÍKLAD 5. Pravděpodobnost zasažení cíle jednou ranou Mírně pozměňme předchozí příklad: místo dvou různých střelců bude na terč střílet stejný střelec. Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: a) bude zasažen třikrát; b) nebude se divit; c) bude udeřeno alespoň jednou; d) bude zasažen přesně jednou. 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 4
Řešení příkladu 5a) Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: a) bude zasažen třikrát; 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 5
Roztok z příkladu 5b) Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: b) nebude zasažen; Rozhodnutí: 02.08.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 6
Řešení příkladu 5c) Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: c) bude zasažen alespoň jednou; Rozhodnutí: 02.08.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 7
Řešení příkladu 5d) Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: d) bude zasažen právě jednou. Rozhodnutí: 02.08.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 8
Poznámka Řešení uvedené v bodě d) příkladu 5 na konkrétním případě opakuje důkaz slavné Bernoulliho věty, která odkazuje na jeden z nejběžnějších pravděpodobnostních modelů: nezávislé opakování stejného testu se dvěma možnými výsledky. Charakteristickým rysem mnoha pravděpodobnostních problémů je, že test, v jehož důsledku může nastat událost, která nás zajímá, se může mnohokrát opakovat. 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 9
V celé sérii opakování je důležité vědět V každém z těchto opakování nás zajímá otázka, zda k této události dojde či nikoliv. A v celé sérii opakování je pro nás důležité přesně vědět, kolikrát k této události může nebo nemusí dojít. Například desetkrát za sebou se házelo kostkou. Jaká je pravděpodobnost, že „čtyřka“ padne přesně 3krát? 10 výstřelů; jaká je pravděpodobnost, že bude přesně 8 zásahů do cíle? Nebo, jaká je pravděpodobnost, že při pěti hozeních mincí přijde na řadu právě 4krát? 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 10
Jacob Bernoulli kombinuje příklady a otázky Švýcarský matematik Jacob Bernoulli z počátku 18. století spojil příklady a otázky tohoto typu do jediného pravděpodobnostního schématu. Nechť pravděpodobnost náhodného jevu A při nějakém testu je rovna P (A). Tento test budeme považovat za test pouze se dvěma možnými výsledky: jedním výsledkem je, že nastane událost A, a druhým výsledkem je, že nenastane událost A, to znamená, že nastane událost Ᾱ. Pro stručnost nazvěme první výsledek (počátek události A) „úspěch“ a druhý výsledek (počátek události Ᾱ) „neúspěch“. Pravděpodobnost P (A) „úspěchu“ bude označena p a pravděpodobnost P (Ᾱ) „neúspěchu“ bude označena q. Proto q = P (Ᾱ) = 1 - P (A) = 1 - p. 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 11
VĚTA 3 (Bernoulliho věta) Věta 3 (Bernoulliho věta). Nechť P n (k) je pravděpodobnost, že přesně k „úspěchů“ nastane v n nezávislých opakováních stejného testu. Pak P n (k) = С n k p k q n-k, kde p je pravděpodobnost „úspěchu“ a q = 1 - p je pravděpodobnost „neúspěchu“ v samostatném testu. Tato věta (uvádíme ji bez důkazu) má velký význam pro teorii i praxi. 02/08/2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 12
PŘÍKLAD 6. Příklad 6. V každé z položek a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost P n (k). a) Jaká je pravděpodobnost, že se při 10 hodech mincí objeví právě 7 „hlav“? b) Každý z 20 lidí samostatně pojmenuje jeden ze dnů v týdnu. "Špatné" dny jsou pondělí a pátek. Jaká je pravděpodobnost, že to „štěstí“ bude přesně poloviční? c) Hod kostkou je „úspěšný“, pokud je hod 5 nebo 6 bodů. Jaká je pravděpodobnost, že přesně 5 z 25 hodů bude „úspěšných“? d) Test spočívá v házení tří různých mincí současně. „Selhání“: existuje více „ocasů“ než „hlav“. Jaká je pravděpodobnost, že mezi 7 hody budou právě tři „štěstí“? 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 13
Řešení 6a) Příklad 6. V každé z položek a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost P n (k). a) Jaká je pravděpodobnost, že se při 10 hodech mincí objeví právě 7 „hlav“? Rozhodnutí: 02.08.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 14
Řešení 6b) Příklad 6. V každé z položek a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost P n (k). b) Každý z 20 lidí samostatně pojmenuje jeden ze dnů v týdnu. "Špatné" dny jsou pondělí a pátek. Jaká je pravděpodobnost, že to „štěstí“ bude přesně poloviční? Rozhodnutí: 02.08.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 15
Řešení 6c) Příklad 6. V každé z položek a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost P n (k). c) Hod kostkou je „úspěšný“, pokud je hod 5 nebo 6 bodů. Jaká je pravděpodobnost, že přesně 5 z 25 hodů bude „úspěšných“? Rozhodnutí: 02.08.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 16
Řešení 6d) Příklad 6. V každé z položek a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost P n (k). d) Test spočívá v házení tří různých mincí současně. „Selhání“: existuje více „ocasů“ než „hlav“. Jaká je pravděpodobnost, že mezi 7 hody budou právě tři „štěstí“? Řešení: d) n = 7, k = 3. „Štěstí“ v jednom hodu spočívá v tom, že „ocasů“ je méně než „hlav“. Celkem je možných 8 výsledků: PPR, PPO, POP, ORR, POO, ORO, OOP, LLC (R - "tails", O - "heads"). Přesně v polovině z nich je méně ocasů: ROO, ORO, OOP, LLC. Tedy p = q = 0,5; P 7 (3) = C 7 3 ∙ 0,5 3 ∙ 0,5 4 = C 7 3 ∙ 0,5 7. 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 17
Bernoulliho teorém umožňuje... Bernoulliho teorém umožňuje navázat spojení mezi statistickým přístupem k definici pravděpodobnosti a klasickou definicí pravděpodobnosti náhodného jevu. Pro popis této souvislosti se vraťme k pojmům v § 50 o statistickém zpracování informací. Zvažte sekvenci n nezávislých opakování stejného pokusu se dvěma výsledky – štěstí a neúspěch. Výsledky těchto testů tvoří řadu dat, která se skládá z určité sekvence dvou možností: „štěstí“ a „neúspěch“. Jednoduše řečeno, existuje posloupnost délky n, složená ze dvou písmen Y ("štěstí") a H ("smůla"). Například U, U, H, H, U, H, H, H, ..., U nebo H, U, U, H, U, U, H, H, U, ..., H atd. n. Vypočítejme násobnost a četnost variant Y, to znamená, že najdeme zlomek k/n, kde k je počet „úspěchů“, se kterými se setkáme mezi všemi n opakováními. Ukazuje se, že při neomezeném nárůstu n bude frekvence k / n výskytu „úspěchů“ prakticky nerozeznatelná od pravděpodobnosti p „úspěchu“ v jednom pokusu. Tento poměrně komplikovaný matematický fakt je odvozen právě z Bernoulliho věty. 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 18
VĚTA 4. Při velkém počtu nezávislých opakování VĚTA 4. Při velkém počtu nezávislých opakování stejného testu se četnost výskytu náhodného jevu A se stále větší přesností přibližně rovná pravděpodobnosti jevu A: k / n ≈ P (A). Například pro n> 2000 s pravděpodobností větší než 99 % lze tvrdit, že absolutní chyba | k / n - P (A) | přibližná rovnost k / n≈ P (A) bude menší než 0,03. V sociologických průzkumech proto stačí vyzpovídat asi 2000 náhodně vybraných lidí (respondentů). Pokud by jich např. na položenou otázku odpovědělo kladně 520, pak k / n = 520/2000 = 0,26 a je prakticky jisté, že pro jakýkoli větší počet respondentů bude tato frekvence v rozmezí od 0,23 do 0,29. Tento jev se nazývá fenomén statistické stability. Bernoulliho věta a její důsledky tedy umožňují (přibližně) najít pravděpodobnost náhodné události v těch případech, kdy její explicitní výpočet není možný. 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 19
Pro učitele 2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 20
2.8.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 21
02.08.2014 Tsybikova Tamara Radnazhapovna, učitelka matematiky 22
Zdroje Algebra a začátek analýzy, ročníky 10-11, 1. část. Učebnice, 10. vydání. (Základní úroveň), A. G. Mordkovich, M., 2009 Algebra a začátek analýzy, ročníky 10-11. (Základní úroveň) Metodická příručka pro učitele, A.G.Mordkovich, P.V.Semenov, M., 2010 Tabulky jsou sestaveny v MS Word a MS Excel. Internetové zdroje Tsybikova Tamara Radnazhapovna, učitelka matematiky 2. 8. 2014 23
Náhled:
Chcete-li použít náhled prezentací, vytvořte si účet Google (účet) a přihlaste se do něj: https://accounts.google.com
Popisky snímků:
Snímek 1
Kapitola 9. Základy matematické statistiky, kombinatoriky a teorie pravděpodobnosti
§54. Náhodné jevy a jejich pravděpodobnosti 3. NEZÁVISLÉ OPAKOVÁNÍ TESTŮ. BERNULLIHO TEORÉM A STATISTICKÁ STABILITA.
Snímek 2
Obsah
PŘÍKLAD 5. Pravděpodobnost zasažení cíle jedním výstřelem ... Řešení 5a); Řešení 5b); Řešení 5c); Řešení 5d) Všimněte si, že ... V celé sérii opakování je důležité vědět ... Jacob Bernoulli spojil příklady a otázky ... VĚTA 3 (Bernoulliho věta).
PŘÍKLAD 6. V každém z bodů a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost Pn (k). Řešení 6a, Řešení 6b); Řešení 6c); Řešení 6d). Bernoulliho věta umožňuje ... VĚTA 4. S velkým počtem nezávislých opakování ... Pro učitele Zdroje.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 3
3. NEZÁVISLÉ OPAKOVÁNÍ TESTŮ. BERNULLIHO TEORÉM A STATISTICKÁ STABILITA.
Část 3.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 4
PŘÍKLAD 5. Pravděpodobnost zasažení cíle jednou ranou
Mírně pozměníme předchozí příklad: místo dvou různých střelců bude na terč střílet stejný střelec Příklad 5. Pravděpodobnost zasažení terče jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: a) bude zasažen třikrát; b) nebude zasažen; c) bude zasažen alespoň jednou; d) bude zasažen přesně jednou.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 5
Řešení příkladu 5a)
Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: a) bude zasažen třikrát;
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 6
Řešení příkladu 5b)
Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: b) nebude zasažen; Řešení:
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 7
Příklad řešení 5c)
Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: c) bude zasažen alespoň jednou; Řešení:
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 8
Příklad řešení 5d)
Příklad 5. Pravděpodobnost zasažení cíle jednou ranou je 0,8. Padly 3 nezávislé výstřely. Najděte pravděpodobnost, že cíl: d) bude zasažen právě jednou. Řešení:
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 9
Poznámka
Řešení uvedené v bodě d) příkladu 5 na konkrétním případě opakuje důkaz slavné Bernoulliho věty, která odkazuje na jeden z nejběžnějších pravděpodobnostních modelů: nezávislé opakování stejného testu se dvěma možnými výsledky. Charakteristickým rysem mnoha pravděpodobnostních problémů je, že test, v jehož důsledku může nastat událost, která nás zajímá, se může mnohokrát opakovat.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 10
Během celého opakování je důležité vědět
V každém z těchto opakování nás zajímá otázka, zda k této události dojde nebo ne. A v celé sérii opakování je pro nás důležité přesně vědět, kolikrát k této události může nebo nemusí dojít. Například desetkrát za sebou se házelo kostkou. Jaká je pravděpodobnost, že „čtyřka“ padne přesně 3krát? 10 výstřelů; jaká je pravděpodobnost, že bude přesně 8 zásahů do cíle? Nebo, jaká je pravděpodobnost, že při pěti hozeních mincí přijde na řadu právě 4krát?
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 11
Jacob Bernoulli spojil příklady a otázky
Jacob Bernoulli, švýcarský matematik z počátku 18. století, spojil příklady a otázky tohoto typu do jediného pravděpodobnostního schématu: Nechť pravděpodobnost náhodného jevu A v nějakém testu je P (A). Tento test budeme považovat za test pouze se dvěma možnými výsledky: jedním výsledkem je, že nastane událost A, a druhým výsledkem je, že nenastane událost A, to znamená, že nastane událost Ᾱ. Pro stručnost nazvěme první výsledek (počátek události A) „úspěch“ a druhý výsledek (počátek události Ᾱ) „neúspěch“. Pravděpodobnost P (A) „úspěchu“ bude označena p a pravděpodobnost P (Ᾱ) „neúspěchu“ bude označena q. Proto q = P (Ᾱ) = 1 - P (A) = 1 - p.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 12
VĚTA 3 (Bernoulliho věta)
Věta 3 (Bernoulliho věta). Nechť Pn (k) je pravděpodobnost, že přesně k „úspěchů“ nastane v n nezávislých opakováních stejného testu. Pak Pn (k) = Сnk pk qn-k, kde р je pravděpodobnost "úspěchu", aq = 1-р je pravděpodobnost "neúspěchu" v samostatném testu. Tato věta (uvádíme bez důkazu) má také velký význam pro teorii a praxi.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 13
PŘÍKLAD 6.
Příklad 6. V každém z bodů a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost Pn (k). lidé nezávisle pojmenovávají jeden z dnů v týdnu. "Špatné" dny jsou pondělí a pátek. Jaká je pravděpodobnost, že bude přesně polovina „štěstí“? Jaká je pravděpodobnost, že právě 5 hodů z 25 bude „úspěšných?“ D) Test spočívá v házení tří různých mincí současně. „Selhání“: existuje více „ocasů“ než „hlav“. Jaká je pravděpodobnost, že mezi 7 hody budou právě tři „štěstí“?
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 14
Řešení 6a)
Příklad 6. V každém z bodů a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost Pn (k).mince? Řešení:
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 15
Řešení 6b)
Příklad 6. V každém z bodů a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost Pn (k). B) Každý z 20 osob samostatně pojmenuje jeden z dnů v týdnu. "Špatné" dny jsou pondělí a pátek. Jaká je pravděpodobnost, že bude přesně poloviční „štěstí“?
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 16
Řešení 6c)
Příklad 6. V každém z bodů a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost Pn (k). C) Hod kostkou je „úspěšný "Pokud padne 5 nebo 6 bodů... Jaká je pravděpodobnost, že přesně 5 z 25 hodů bude „úspěšných“?
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 17
Řešení 6d)
Příklad 6. V každém z bodů a) - d) určete hodnoty n, k, p, q a napište (bez výpočtů) výraz pro požadovanou pravděpodobnost Pn (k). D) Test spočívá v současném házení tří různých mincí. „Selhání“: existuje více „ocasů“ než „hlav“. Jaká je pravděpodobnost, že mezi 7 hody budou právě tři „zásahy"? Řešení: d) n = 7, k = 3. „Štěstí" v jednom hodu je, že je méně „ocasů" než „hlav". Celkem je možných 8 výsledků: PPR, PPO, POP, ORR, POO, ORO, OOP, LLC (R - "tails", O - "heads"). Přesně v polovině z nich je méně ocasů: ROO, ORO, OOP, LLC. Tedy p = q = 0,5; Р7 (3) = С73 ∙ 0,53 ∙ 0,54 = С73 ∙ 0,57.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 18
Bernoulliho věta umožňuje...
Bernoulliho věta umožňuje vytvořit souvislost mezi statistickým přístupem k definici pravděpodobnosti a klasickou definicí pravděpodobnosti náhodné události. Pro popis této souvislosti se vraťme k pojmům v § 50 o statistickém zpracování informací. Zvažte sekvenci n nezávislých opakování stejného pokusu se dvěma výsledky – štěstí a neúspěch. Výsledky těchto testů tvoří řadu dat, která se skládá z určité sekvence dvou možností: „štěstí“ a „neúspěch“. Jednoduše řečeno, existuje posloupnost délky n, složená ze dvou písmen Y ("štěstí") a H ("smůla"). Například U, U, H, H, U, H, H, H, ..., U nebo H, U, U, H, U, U, H, H, U, ..., H atd. n. Vypočítejme násobnost a četnost variant Y, to znamená, že najdeme zlomek k/n, kde k je počet „úspěchů“, se kterými se setkáme mezi všemi n opakováními. Ukazuje se, že při neomezeném nárůstu n bude frekvence k / n výskytu „úspěchů“ prakticky nerozeznatelná od pravděpodobnosti p „úspěchu“ v jednom pokusu. Tento poměrně komplikovaný matematický fakt je odvozen právě z Bernoulliho věty.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 19
VĚTA 4. Pro velký počet nezávislých opakování
VĚTA 4. Při velkém počtu nezávislých opakování stejného testu se četnost výskytu náhodného jevu A se stále větší přesností přibližně rovná pravděpodobnosti jevu A: k / n≈ P (A). pro n> 2000 s pravděpodobností větší než 99 % lze tvrdit, že absolutní chyba |k / n- P (A) | přibližná rovnost k / n≈ P (A) bude menší než 0,03. V sociologických průzkumech proto stačí vyzpovídat asi 2000 náhodně vybraných lidí (respondentů). Pokud by jich např. na položenou otázku odpovědělo kladně 520, pak k / n = 520/2000 = 0,26 a je prakticky jisté, že pro jakýkoli větší počet respondentů bude tato frekvence v rozmezí od 0,23 do 0,29. Tento jev se nazývá fenomén statistické stability, Bernoulliho věta a její důsledky tedy umožňují (přibližně) najít pravděpodobnost náhodné události v těch případech, kdy její explicitní výpočet není možný.
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 20
Pro učitele
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 21
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 22
08.02.2014
Tsybikova Tamara Radnazhapovna, učitelka matematiky
*
Snímek 23
Zdroje
Algebra a začátek analýzy, ročníky 10-11, 1. část. Učebnice, 10. vydání. (Základní úroveň), A. G. Mordkovich, M., 2009 Algebra a začátek analýzy, ročníky 10-11. (Základní úroveň) Metodická příručka pro učitele, A.G.Mordkovich, P.V.Semenov, M., 2010 Tabulky jsou sestaveny v MS Word a MS Excel Internetové zdroje
Tsybikova Tamara Radnazhapovna, učitelka matematiky
08.02.2014
*
Bernoulliho vzorec
Belyaeva T.Yu. GBPOU CC "AMT", Armavir Učitel matematiky

- Jeden ze zakladatelů teorie pravděpodobnosti a matematické analýzy
- Zahraniční člen Pařížské akademie věd (1699) a Berlínské akademie věd (1701)
Starší bratr Johanna Bernoulliho (nejslavnějšího člena rodiny Bernoulli)
Jacob Bernoulli (1654-1705)
švýcarský matematik

Ať se vyrábí P nezávislé pokusy, v každém z nich je pravděpodobnost, že událost A nastane R , a proto pravděpodobnost, že se to nestane, je q = 1 - p .
Je potřeba najít pravděpodobnost, že pro P událost A po sobě jdoucích testů nastane přesně T jednou.
Požadovaná pravděpodobnost je označena R P ( T ) .

To je zřejmé
p 1 (1) = p, p 1 (0) = q
R 1 (1) + str 1 (0) = p + q = 1

- Ve dvou testech:
Možné jsou 4 výsledky:
p2(2) = p2; p2(1) = 2pq; p2(0) = q2
R 2 (2) + str 2 (1) + str 2 (0) = (p + q) 2 = 1

- Ve třech testech:
8 možných výsledků:
Dostaneme:
p 3 (2) = 3p 2 q
p 3 (1) = 3 pq 2
R 3 (3) + str 3 (2) + str 3 (1) + str 3 (0) = (p + q) 3 = 1


Cíl 1
Mince je hozena 8krát. Jaká je pravděpodobnost, že „erb“ padne 4x?

Cíl 2
V urně je 20 míčků: 15 bílých a 5 černých. Vyndali 5 míčků v řadě, přičemž každý odebraný míček se vrátil do urny, než odebral další míč. Najděte pravděpodobnost, že z pěti vytažených koulí budou 2 bílé koule.

Vzorce pro zjištění pravděpodobnosti, že proti P zkušební akce přijde :
A) méně než tkrát
R P (0) + ... + str P (t-1)
b) více než tkrát
R P (m + 1) + ... + str P (P)
proti) ne více než tkrát
R P (0) + ... + str P (T)
G) alespoň tkrát
R P (t) + ... + str P (P)

Cíl 3
Pravděpodobnost výroby nestandardního dílu na automatickém stroji je 0,02. Určete pravděpodobnost, že mezi náhodně odebranými šesti díly budou více než 4 standardní.
Událost A - « více než 4 standardní díly"(5 nebo 6) znamená
« ne více než 1 vadný díl"(0 nebo 1)

Ať se vyrábí P nezávislé testy. U každého takového testu může, ale nemusí nastat událost A. Pravděpodobnost výskytu události A.
Je nutné takové číslo najít μ (0, 1, ..., n), pro které bude pravděpodobnost P n (μ) nejvyšší.


Úkol 4.
Podíl prémiových produktů v tomto podniku je 31 %. Jaký je nejpravděpodobnější počet položek „Navíc“, pokud je vybrána dávka 75 položek?
Podle podmínky: n = 75, p = 0,31, q = 1 - 0,31 = 0,69


Úkol 6.
Dva střelci střílejí na cíl. Pravděpodobnost neúspěchu v jednom výstřelu pro prvního střelce je 0,2 a pro druhého - 0,4. Najděte nejpravděpodobnější počet salv, které nezasáhnou cíl, pokud střelci vystřelí 25 salv.
Podle podmínky: n = 25, p = 0,2 0,4 = 0,08, q = 0,92
Opakované nezávislé studie se nazývají Bernoulliho studie, pokud každá studie má pouze dva možné výsledky a pravděpodobnosti výsledků zůstávají u všech studií stejné.
Označme tyto pravděpodobnosti jako p a q... Výsledek s pravděpodobností p se bude nazývat „úspěch“ a výsledek s pravděpodobností q- "selhání".
To je zřejmé
Základní prostor pro každou zkoušku se skládá ze dvou bodů. Prostor elementárních akcí pro n Bernoulliho test obsahuje body, z nichž každý představuje jeden možný výsledek složeného experimentu. Vzhledem k tomu, že pokusy jsou nezávislé, je pravděpodobnost sledu událostí rovna součinu pravděpodobností odpovídajících výsledků. Například pravděpodobnost sledu událostí
(U, U, H, U, H, H, H)
rovnající se produktu
Příklady Bernoulliho testů.
1. Postupné házení „správné“ mince. V tomto případě p = q = 1/2 .
Když je vržena asymetrická mince, odpovídající pravděpodobnosti změní své hodnoty.
2. Každý výsledek experimentu lze považovat za A nebo .
3. Existuje-li několik možných výsledků, lze od nich odlišit skupinu výsledků, které jsou považovány za „úspěch“, přičemž všechny ostatní výsledky se nazývají „selhání“.
Například při postupných hodech kostkou lze „úspěch“ chápat jako hod 5 a „neúspěch“ - pád jakéhokoli jiného počtu bodů. V tomto případě p = 1/6, q = 5/6.
Pokud „úspěchem“ rozumíme ztrátu sudého čísla a „neúspěchem“ - lichým počtem bodů, pak p = q = 1/2 .
4. Opakované náhodné vytažení míčku z urny obsahující při každém testu A bílý písek bčerné koule. Pokud úspěchem myslíme extrakci bílé koule, pak,.
Feller uvádí následující příklad praktické aplikace Bernoulliho testovacího schématu. Podložky vyrobené v sériové výrobě se mohou lišit tloušťkou, ale při kontrole jsou klasifikovány jako dobré nebo vadné v závislosti na tom, zda je tloušťka v předepsaných mezích. Ačkoli výrobky z mnoha důvodů nemusí plně odpovídat Bernoulliho schématu, toto schéma stanoví ideální standard pro průmyslovou kontrolu kvality výrobků, i když tohoto standardu není nikdy zcela přesně dosaženo. Stroje podléhají změnám, a proto pravděpodobnosti nezůstávají stejné; existuje určitá konzistence v provozním režimu strojů, v důsledku čehož jsou dlouhé série identických odchylek pravděpodobnější, než by tomu bylo, kdyby testy byly skutečně nezávislé. Z hlediska kontroly kvality produktu je však žádoucí, aby se proces řídil Bernoulliho schématem, a je důležité, aby toho bylo možné dosáhnout v rámci určitých mezí. Účelem monitorování je včas odhalit významné odchylky od ideálního schématu a použít je jako indikátory hrozícího porušení správného provozu stroje.
"Prvky matematické statistiky" - Interval spolehlivosti. Věda. Klasifikace hypotéz. Díly jsou vyráběny na různých strojích. Pravidla validace. Korelační závislost. Závislost. Sada hodnot kritéria. Najděte interval spolehlivosti. Výpočet intervalů spolehlivosti pro neznámý rozptyl. Normální distribuce.
"Pravděpodobnost a matematická statistika" - Přesnost získaných hodnot. Bezpečná šifra. Deskriptivní statistika. Jablko. Zvažte události. Pravidlo násobení. Dvě šipky. Porovnání tréninkových programů. Karamel. Příklady sloupcových grafů. Matematické známky. Pravidlo násobení pro tři. Bílé a červené růže. 9 různých knih. Zimní prázdniny.
"Základy matematické statistiky" - podmíněná pravděpodobnost. Tabulka standardizovaných hodnot. Vlastnosti Studentova rozdělení. Interval spolehlivosti matematického očekávání. Ukázkový průměr. Rozdělení. Jeden test lze považovat za sérii jednoho testu. Kvantil - vlevo by měl být počet hodnot odpovídajících kvantilovému indexu.
"Teorie pravděpodobnosti a statistika" - Hranice intervalu. Kritické oblasti. Věta o násobení pravděpodobnosti. Rozdělení normální náhodné veličiny. Odvození Bernoulliho vzorce. Distribuční zákony náhodných veličin. Formulace ZBCH. Význam a formulace centrální limitní věty. Vztah jmenných znaků. Stochastická závislost dvou náhodných veličin.
"Statistický výzkum" - Relevance. Statistické charakteristiky a výzkum. Plán. Swing je rozdíl mezi největší a nejmenší hodnotou v datové řadě. Typy statického pozorování. Baví tě studovat matematiku. Zvažte řadu čísel. Kdo vám pomůže vyřešit obtížné téma v matematice. Potřebujete matematiku ve své budoucí profesi?
"Základní statistické charakteristiky" - Základní statistické charakteristiky. Najděte aritmetický průměr. Petronius. Výpad. Řádková móda. Aritmetický průměr řady čísel. Rozsah série. Medián série. Statistika. Medián. Školní sešity.
Celkem je 17 prezentací
FEDERÁLNÍ VZDĚLÁVACÍ AGENTURA
Státní vzdělávací instituce
vyšší odborné vzdělání
"MATI" RUSKÁ STÁTNÍ TECHNOLOGICKÁ UNIVERZITA IM. K.E. TSIOLKOVSKÝ
Katedra "Modelování systémů a informačních technologií"
Opakování testů. Bernoulliho schéma
Metodické pokyny k praktickým cvičením
v oboru "Vyšší matematika"
Sestavil: Egorova Yu.B.
Mamonov I.M.
Moskva 2006 úvod
Metodické pokyny jsou určeny studentům denních a večerních kateder fakulty č. 14 oborů 150601, 160301, 230102. Pokyny zvýrazňují základní pojmy tématu, určují posloupnost studia látky. K praktickému zvládnutí tématu napomáhá velké množství uvažovaných příkladů. Metodické pokyny slouží jako metodický základ pro praktický nácvik a individuální zadání.
BERNULLYHO SCHÉMA. FORMULE BERNULLI
Bernoulliho schéma- schéma opakovaných nezávislých testů, při kterých se event A lze opakovat mnohokrát s konstantní pravděpodobností R (A)= R .
Příklady testů prováděných podle Bernoulliho schématu: opakované házení mincí nebo kostkou, výroba dávky dílů, střelba na cíl atd.
Teorém. Pokud je pravděpodobnost výskytu události A v každém testu je konstantní a rovna R, pak pravděpodobnost, že událost A přijde m jednou v n testy (bez ohledu na to, v jakém pořadí), lze určit podle Bernoulliho vzorce:

kde q = 1 – p.
PŘÍKLAD 1. Pravděpodobnost, že spotřeba elektřiny během jednoho dne nepřekročí stanovenou sazbu, se rovná p = 0,75. Najděte pravděpodobnost, že v následujících 6 dnech spotřeba energie po dobu 4 dnů nepřekročí normu.
ŘEŠENÍ. Pravděpodobnost běžné spotřeby elektřiny během každého ze 6 dnů je konstantní a rovná se R= 0,75. Pravděpodobnost nadměrné spotřeby elektřiny za den je tedy také konstantní a rovná q = 1R = 1 0,75 = 0,25.
Požadovaná pravděpodobnost podle Bernoulliho vzorce je:
PŘÍKLAD 2 Střelec vypálí tři rány na cíl. Pravděpodobnost zásahu cíle při každém výstřelu je p = 0,3. Najděte pravděpodobnost, že: a) je zasažen jeden cíl; b) všechny tři cíle; c) ani jeden cíl; d) alespoň jeden cíl; e) méně než dva cíle.
ŘEŠENÍ. Pravděpodobnost zásahu cíle při každém výstřelu je konstantní a rovná se R= 0,75. Pravděpodobnost neúspěchu tedy je q = 1 R= 1 0,3 = 0,7. Celkový počet provedených experimentů n=3.
a) Pravděpodobnost zasažení jednoho cíle třemi ranami se rovná:
b) Pravděpodobnost zasažení všech tří terčů třemi ranami je rovna:
c) Pravděpodobnost tří chyb na tři rány se rovná:
d) Pravděpodobnost zasažení alespoň jednoho cíle třemi ranami je rovna:
e) Pravděpodobnost zasažení méně než dvou cílů, to znamená buď jednoho nebo žádného:
Lokální a integrální Moivre-Laplaceovy věty
Pokud se provádí velké množství testů, pak se výpočet pravděpodobností pomocí Bernoulliho vzorce stává technicky obtížným, protože vzorec vyžaduje operace s velkými čísly. Proto existují jednodušší přibližné vzorce pro výpočet pravděpodobností obecně n... Tyto vzorce se nazývají asymptotické a jsou určeny Poissonovou větou, lokální a integrální Laplaceovou větou.
Lokální Moivre-Laplaceova věta. A A se stane m jednou v n n (n →∞ ) se přibližně rovná:

kde funkce  a argument
a argument 
Více n, tím přesnější je výpočet pravděpodobností. Proto je účelné aplikovat Moivre-Laplaceovu větu pro npq 20.
F ( X ) sestavené speciální tabulky (viz příloha 1). Při použití stolu mějte na paměti vlastnosti funkce f (x) :
Funkce f (x) je sudý f ( x) = f (x) .
Na X ∞ funkce f (x) 0. V praxi můžeme předpokládat, že již při X> 4 funkce f (x) ≈0.
PŘÍKLAD 3 Najděte pravděpodobnost, že událost A se vyskytuje 80krát ve 400 výzvách, pokud je pravděpodobnost výskytu události A v každém pokusu se rovná p = 0,2.
ŘEŠENÍ. Podle podmínek n=400, m=80, p=0,2, q= 0,8. Proto:

Pomocí tabulky určíme hodnotu funkce F (0)=0,3989.
Moivre-Laplaceova integrální věta. Pokud je pravděpodobnost výskytu události A v každém testu je konstantní a liší se od 0 a 1, pak pravděpodobnost, že událost A bude pocházet z m 1 před m 2 jednou v n testy s dostatečně velkým počtem n (n →∞ ) se přibližně rovná:
kde  integrál nebo Laplaceova funkce,
integrál nebo Laplaceova funkce, 

Chcete-li najít hodnoty funkce F ( X ) sestavené speciální tabulky (např. viz příloha 2). Při použití stolu mějte na paměti vlastnosti Laplaceovy funkce Ф (x) :
Funkce Ф (x) je lichý F ( x) = Ф (x) .
Na X ∞ funkce Ф (x) 0,5. V praxi můžeme předpokládat, že již v X> 5 funkcí Ф (x) ≈0,5.
F (0)=0.
PŘÍKLAD 4. Pravděpodobnost, že díl neprošel kontrolou QCD, je 0,2. Najděte pravděpodobnost, že mezi 400 díly bude 70 až 100 netestovaných.
ŘEŠENÍ. Podle podmínek n=400, m 1 =70, m 2 =100, p=0,2, q= 0,8. Proto:


Podle tabulky, ve které jsou uvedeny hodnoty Laplaceovy funkce, určíme:
Ф (x 1 ) = F ( 1,25 )= F ( 1,25 )= 0,3944; Ф (x 2 ) = F ( 2,5 )= 0,4938.





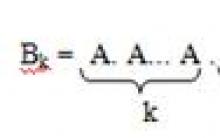




Symboly topografických map
Mimoškolní aktivity „mapa je druhým jazykem zeměpisu“
Literární hra na motivy pohádek pro děti 1. stupně ZŠ Knižní kolotoč literární hra pro 1. stupeň ZŠ
Prezentace pro hru na hrdiny "Poliklinika" Prezentace spiknutí domácí lékař na lodi dhow
"Vlastní hra" (Vše o novém roce) Soutěže ve formě prezentace na nový rok