Distinguish between dependent and independent events. Two events are said to be independent if the occurrence of one of them does not change the probability of the occurrence of the other. For example, if two automatic lines operate in a workshop, which are not interconnected according to production conditions, then the stops of these lines are independent events.
Several events are called collectively independent, if any of them does not depend on any other event and on any combination of the others.
The events are called dependent, if one of them affects the probability of occurrence of the other. For example, two production plants are connected by a single technological cycle. Then the probability of failure of one of them depends on the state of the other. The probability of one event B, calculated assuming the occurrence of another event A, is called conditional probability event B and is denoted by P(A|B).
The condition for the independence of the event B from the event A is written as P(B|A)=P(B), and the condition for its dependence as P(B|A)≠P(B).
Probability of an event in Bernoulli trials. Poisson formula.
Repeated independent tests, Bernoulli trials or Bernoulli scheme such trials are called if for each trial there are only two outcomes - the occurrence of event A or and the probability of these events remains unchanged for all trials. This simple scheme of random trials is of great importance in probability theory.
The most famous example of Bernoulli's trials is the experiment with successive tossing of a regular (symmetrical and homogeneous) coin, where the event A is the loss, for example, of a "coat of arms" ("tails").
Let in some experience the probability of event A is equal to P(A)=p, then , where р+q=1. Let's run the experiment n times, assuming that the individual trials are independent, which means that the outcome of any of them is not related to the outcomes of previous (or subsequent) trials. Let's find the probability of occurrence of events A exactly k times, say only in the first k trials. Let be an event that, in n trials, event A will occur exactly k times in the first trials. The event can be represented as

Since we assumed the experiments to be independent, then
41)[page2] If we raise the question of the occurrence of event A k-times in n trials in an arbitrary order, then the event can be represented as
The number of different terms on the right side of this equality is equal to the number of trials from n to k, so the probability of events, which we will denote, is equal to
The sequence of events forms a complete group of independent events ![]() . Indeed, from the independence of events, we obtain
. Indeed, from the independence of events, we obtain
Independent events
In the practical application of probabilistic-statistical decision-making methods, the concept of independence is constantly used. For example, when applying statistical methods of product quality management, one speaks of independent measurements of the values of controlled parameters for the units of production included in the sample, of the independence of the appearance of defects of one type from the appearance of defects of another type, etc. The independence of random events is understood in probabilistic models in the following sense.
Definition 2. Events A and V are called independent if P(AB) = P(A) P(B). Multiple events A, V, WITH,… are called independent if the probability of their joint implementation is equal to the product of the probabilities of each of them separately: R(ABC…) = R(A)R(V)R(WITH)…
This definition corresponds to the intuitive notion of independence: the occurrence or non-occurrence of one event should not affect the occurrence or non-occurrence of another. Sometimes the ratio R(AB) = R(A) R(V|A) = P(B)P(A|B), valid for P(A)P(B) > 0, also called the probability multiplication theorem.
Statement 1. Let the events A and V independent. Then the events and are independent, the events and V independent, events A and independent (here is the event opposite A, and - an event opposite V).
Indeed, it follows from property c) in (3) that for events WITH and D, whose product is empty, P(C+ D) = P(C) + P(D). Since the intersection AB and V is empty, but there is a union V, then P(AB) + P(B) = P(B). Since A and B are independent, then P(B) = P(B) - P(AB) = P(B) - P(A)P(B) = P(B)(1 - P(A)). Note now that relations (1) and (2) imply that P() = 1 - P(A). Means, P(B) = P()P(B).
Equality derivation P(A) = P(A)P() differs from the previous one only by the replacement everywhere A on the V, a V on the A.
To prove independence and Let's take advantage of the fact that events AB, B, A, do not have pairwise common elements, but in total they constitute the entire space of elementary events. Hence, R(AB) + P(B) + P(A) + P() = 1. Using the above relations, we get that P(B)= 1 -R(AB) - P(B)( 1 - P(A)) - P(A)( 1 - P(B))=( 1 – P(A))( 1 – P(B)) = P()P(), which was to be proved.
Example 3 Consider the experience of throwing a dice with the numbers 1, 2, 3, 4, 5,6 written on the sides. We assume that all faces have the same chance of being at the top. Let us construct the corresponding probability space. Let us show that the events “above is a face with an even number” and “above is a face with a number divisible by 3” are independent.
Parsing an example. The space of elementary outcomes consists of 6 elements: “above – face with 1”, “above – face with 2”,…, “above – face with 6”. The event "on top - face with an even number" consists of three elementary events - when 2, 4 or 6 is on top. The event "on top - face with a number divisible by 3" consists of two elementary events - when 3 or 6 is on top. all faces have the same chance of being on top, then all elementary events must have the same probability. Since there are 6 elementary events in total, each of them has a probability of 1/6. By definition 1, the event “on top is a face with an even number” has a probability of 1/2, and the event “on top is a face with a number divisible by 3” has a probability of 1/3. The product of these events consists of one elementary event “above - the edge with 6”, and therefore has a probability of 1/6. Since 1/6 = ½ x 1/3, the events in question are independent according to the definition of independence.
If, at the occurrence of an event, the probability of an event  does not change, then the events
does not change, then the events  and
and  called independent.
called independent.
Theorem:Probability of joint occurrence of two independent events  and
and  (works
(works  and
and  ) is equal to the product of the probabilities of these events.
) is equal to the product of the probabilities of these events.
Indeed, since
events  and
and  independent, then
independent, then  . In this case, the formula for the probability of a product of events
. In this case, the formula for the probability of a product of events  and
and  takes the form.
takes the form.
Events  called pairwise independent if any two of them are independent.
called pairwise independent if any two of them are independent.
Events  called collectively independent (or simply independent), if every two of them are independent and each event and all possible products of the others are independent.
called collectively independent (or simply independent), if every two of them are independent and each event and all possible products of the others are independent.
Theorem:Probability of product of a finite number of independent events in the aggregate
 is equal to the product of the probabilities of these events.
is equal to the product of the probabilities of these events.
Let us illustrate the difference in the application of the event probability formulas for dependent and independent events using examples
Example 1. The probability of hitting the target by the first shooter is 0.85, the second is 0.8. The guns fired one shot at a time. What is the probability that at least one projectile hit the target?
Solution: P(A+B) =P(A) +P(B) –P(AB) Since the shots are independent, then
P(A+B) = P(A) +P(B) –P(A)*P(B) = 0.97
Example 2. An urn contains 2 red and 4 black balls. 2 balls are taken out of it in a row. What is the probability that both balls are red.
Solution: 1 case. Event A - the appearance of a red ball at the first removal, event B - at the second. Event C is the appearance of two red balls.
P(C) \u003d P (A) * P (B / A) \u003d (2/6) * (1/5) \u003d 1/15
2nd case. The first ball drawn is returned to the basket.
P(C) \u003d P (A) * P (B) \u003d (2/6) * (2/6) \u003d 1/9
Total Probability Formula.
Let the event  can only happen to one of the incompatible events
can only happen to one of the incompatible events
 , forming a complete group. For example, the store receives the same products from three enterprises and in different quantities. The probability of producing low-quality products at these enterprises is different. One of the products is randomly selected. It is required to determine the probability that this product is of poor quality (event
, forming a complete group. For example, the store receives the same products from three enterprises and in different quantities. The probability of producing low-quality products at these enterprises is different. One of the products is randomly selected. It is required to determine the probability that this product is of poor quality (event  ). Events here
). Events here
 - this is the choice of a product from the products of the corresponding enterprise.
- this is the choice of a product from the products of the corresponding enterprise.
In this case, the probability of the event  can be considered as the sum of products of events
can be considered as the sum of products of events  .
.
By the addition theorem for the probabilities of incompatible events, we obtain  . Using the probability multiplication theorem, we find
. Using the probability multiplication theorem, we find
 .
.
The resulting formula is called total probability formula.
Bayes formula
Let the event  happens at the same time as one of
happens at the same time as one of  incompatible events
incompatible events
 , whose probabilities
, whose probabilities  (
( ) are known before experience ( a priori probabilities). An experiment is performed, as a result of which the occurrence of an event is registered
) are known before experience ( a priori probabilities). An experiment is performed, as a result of which the occurrence of an event is registered  , and it is known that this event had certain conditional probabilities
, and it is known that this event had certain conditional probabilities  (
( ). It is required to find the probabilities of events
). It is required to find the probabilities of events  if the event is known
if the event is known  happened ( a posteriori probabilities).
happened ( a posteriori probabilities).
The problem is that, having new information (event A has occurred), it is necessary to overestimate the probabilities of events
 .
.
Based on the theorem on the probability of the product of two events

 .
.
The resulting formula is called Bayes formulas.
Basic concepts of combinatorics.
When solving a number of theoretical and practical problems, it is required to make various combinations from a finite set of elements according to given rules and to count the number of all possible such combinations. Such tasks are called combinatorial.
When solving problems, combinatorics use the rules of sum and product.
When assessing the probability of the occurrence of any random event, it is very important to have a good idea in advance whether the probability (probability of the event) of the occurrence of the event of interest to us depends on how other events develop. In the case of the classical scheme, when all outcomes are equally probable, we can already estimate the probability values of the individual event of interest to us on our own. We can do this even if the event is a complex collection of several elementary outcomes. And if several random events occur simultaneously or sequentially? How does this affect the probability of the event of interest to us? If I roll a die a few times and want to get a six and I'm not lucky all the time, does that mean I should increase my bet because, according to probability theory, I'm about to get lucky? Alas, probability theory says nothing of the sort. Neither dice, nor cards, nor coins can remember what they showed us last time. It does not matter to them at all whether for the first time or for the tenth time today I test my fate. Every time I roll again, I know only one thing: and this time the probability of rolling a "six" again is one-sixth. Of course, this does not mean that the number I need will never fall out. It only means that my loss after the first toss and after any other toss are independent events. Events A and B are called independent if the realization of one of them does not affect the probability of the other event in any way. For example, the probabilities of hitting a target with the first of two guns do not depend on whether the other gun hit the target, so the events "the first gun hit the target" and "the second gun hit the target" are independent. If two events A and B are independent, and the probability of each of them is known, then the probability of the simultaneous occurrence of both event A and event B (denoted by AB) can be calculated using the following theorem.
Probability multiplication theorem for independent events
P(AB) = P(A)*P(B) the probability of the simultaneous occurrence of two independent events is equal to the product of the probabilities of these events.
Example 1. The probabilities of hitting the target when firing the first and second guns are respectively equal: p 1 = 0.7; p2 = 0.8. Find the probability of hitting with one volley by both guns simultaneously.
As we have already seen, the events A (hit by the first gun) and B (hit by the second gun) are independent, i.e. P(AB)=P(A)*P(B)=p1*p2=0.56. What happens to our estimates if the initiating events are not independent? Let's change the previous example a little.
Example 2 Two shooters in a competition shoot at targets, and if one of them shoots accurately, then the opponent starts to get nervous, and his results worsen. How to turn this everyday situation into a mathematical problem and outline ways to solve it? It is intuitively clear that it is necessary to somehow separate the two scenarios, to compose, in fact, two scenarios, two different tasks. In the first case, if the opponent misses, the scenario will be favorable for the nervous athlete and his accuracy will be higher. In the second case, if the opponent decently realized his chance, the probability of hitting the target for the second athlete is reduced. To separate the possible scenarios (they are often called hypotheses) of the development of events, we will often use the "probability tree" scheme. This diagram is similar in meaning to the decision tree, which you have probably already had to deal with. Each branch is a separate scenario, only now it has its own value of the so-called conditional probability (q 1 , q 2 , q 1 -1, q 2 -1).
This scheme is very convenient for the analysis of successive random events. It remains to clarify one more important question: where do the initial values of probabilities come from in real situations? After all, the theory of probability does not work with the same coins and dice, does it? Usually these estimates are taken from statistics, and when statistics are not available, we conduct our own research. And we often have to start it not with collecting data, but with the question of what information we generally need.
Example 3 In a city of 100,000 inhabitants, suppose we need to estimate the size of the market for a new non-essential product, such as a color-treated hair conditioner. Let's consider the "tree of probabilities" scheme. In this case, we need to approximately estimate the value of the probability on each "branch". So, our estimates of market capacity:
1) 50% of all residents of the city are women,
2) of all women, only 30% dye their hair often,
3) of these, only 10% use balms for colored hair,
4) of these, only 10% can muster up the courage to try a new product,
5) 70% of them usually buy everything not from us, but from our competitors.

According to the law of multiplication of probabilities, we determine the probability of the event of interest to us A = (a resident of the city buys this new balm from us) = 0.00045. Multiply this probability value by the number of inhabitants of the city. As a result, we have only 45 potential buyers, and given that one vial of this product is enough for several months, the trade is not very lively. Still, there are benefits from our assessments. Firstly, we can compare the forecasts of different business ideas, they will have different “forks” on the diagrams, and, of course, the probability values will also be different. Secondly, as we have already said, a random variable is not called random because it does not depend on anything at all. It's just that its exact meaning is not known in advance. We know that the average number of buyers can be increased (for example, by advertising a new product). So it makes sense to focus on those "forks" where the distribution of probabilities does not particularly suit us, on those factors that we are able to influence. Consider another quantitative example of consumer behavior research.
Example 3 An average of 10,000 people visit the food market per day. The probability that a market visitor walks into a dairy pavilion is 1/2. It is known that in this pavilion, on average, 500 kg of various products are sold per day. Can it be argued that the average purchase in the pavilion weighs only 100 g?
Discussion.
Of course not. It is clear that not everyone who entered the pavilion ended up buying something there.

As shown in the diagram, in order to answer the question about the average purchase weight, we must find the answer to the question, what is the probability that a person who enters the pavilion buys something there. If we do not have such data at our disposal, but we need them, we will have to obtain them ourselves, after observing the visitors of the pavilion for some time. Suppose our observations show that only a fifth of the visitors to the pavilion buy something. As soon as these estimates are obtained by us, the task becomes already simple. Of the 10,000 people who came to the market, 5,000 will go to the pavilion of dairy products, there will be only 1,000 purchases. The average purchase weight is 500 grams. It is interesting to note that in order to build a complete picture of what is happening, the logic of conditional "branching" must be defined at each stage of our reasoning as clearly as if we were working with a "concrete" situation, and not with probabilities.
Tasks for self-examination.
1. Let there be an electrical circuit consisting of n series-connected elements, each of which operates independently of the others. The probability p of non-failure of each element is known. Determine the probability of proper operation of the entire section of the circuit (event A).

2. The student knows 20 of the 25 exam questions. Find the probability that the student knows the three questions given to him by the examiner.
3. Production consists of four successive stages, each of which operates equipment for which the probabilities of failure during the next month are, respectively, p 1 , p 2 , p 3 and p 4 . Find the probability that in a month there will be no stoppage of production due to equipment failure.
In the USE assignments in mathematics, there are also more complex probability problems (than we considered in Part 1), where you have to apply the rule of addition, multiplication of probabilities, and distinguish between joint and incompatible events.
So, theory.
Joint and non-joint events
Events are said to be incompatible if the occurrence of one of them excludes the occurrence of the others. That is, only one particular event can occur, or another.
For example, by throwing a die, you can distinguish between events such as an even number of points and an odd number of points. These events are incompatible.
Events are called joint if the occurrence of one of them does not exclude the occurrence of the other.
For example, when throwing a die, you can distinguish between events such as the occurrence of an odd number of points and the loss of a number of points that is a multiple of three. When three is rolled, both events are realized.
Sum of events
The sum (or union) of several events is an event consisting in the occurrence of at least one of these events.
Wherein the sum of two disjoint events is the sum of the probabilities of these events:
For example, the probability of getting 5 or 6 points on a dice in one throw will be because both events (drop 5, drop 6) are incompatible and the probability of one or the second event is calculated as follows:
The probability the sum of two joint events is equal to the sum of the probabilities of these events without taking into account their joint occurrence:
For example, in a shopping mall, two identical vending machines sell coffee. The probability that the machine will run out of coffee by the end of the day is 0.3. The probability that both machines will run out of coffee is 0.12. Let's find the probability that by the end of the day coffee will end in at least one of the machines (that is, either in one, or in the other, or in both at once).
 The probability of the first event "coffee will end in the first machine" as well as the probability of the second event "coffee will end in the second machine" by the condition is equal to 0.3. Events are collaborative.
The probability of the first event "coffee will end in the first machine" as well as the probability of the second event "coffee will end in the second machine" by the condition is equal to 0.3. Events are collaborative.
The probability of the joint realization of the first two events is equal to 0.12 according to the condition.
This means that the probability that by the end of the day the coffee will run out in at least one of the machines is
Dependent and independent events
Two random events A and B are called independent if the occurrence of one of them does not change the probability of the other occurring. Otherwise, events A and B are called dependent.
For example, when two dice are rolled at the same time, one of them, say 1, and the other 5, are independent events.
Product of probabilities
A product (or intersection) of several events is an event consisting in the joint occurrence of all these events.
If there are two independent events A and B with probabilities P(A) and P(B), respectively, then the probability of the realization of events A and B is simultaneously equal to the product of the probabilities:
For example, we are interested in the loss of a six on a dice twice in a row. Both events are independent and the probability of each of them occurring separately is . The probability that both of these events will occur will be calculated using the above formula: .
See a selection of tasks for working out the topic.



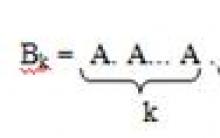





Map second language of geography
Literary games in elementary school Games for children in the library elementary school
Presentation "role-playing games in dow"
The green color on the physical map shows what the colors on the physical map represent
Intellectual game "through the pages of history"